طراحی بهینه ( روش طراحی پارامتریک)

ACCESS TO RELEVANT DATA is essential for high-quality, fact-based decisionmaking.
While engineers have always approached their work in this manner, the modern project workflow has brought about a specific, significant change. Client expectations have grown beyond the concept of a “final” deliverable to now include a continuous influx of data upon which they base key business decisions. In other words, engineers are now purveyors of data just as much as they are consumers of it.
In the field of structural engineering, the potential data includes, but is not limited to: structural steel tonnage associated with various framing configurations, economies of scale projections for repetitive connection types, and the relationship between steel tonnage and occupancy comfort for various serviceability considerations. The relevant data varies for each project, and engineers have a powerful tool to efficiently acquire the data most useful to a given project: parametric design.
While this approach has been around for roughly a decade, it’s not particularly widespread. But it can prove to be exceptionally useful. Depending on the complexity of the problem, engineers can automate millions of simulations, process data, and have presentation-ready graphics in a matter of hours. Here, we’ll cover three real-world examples that used parametric design to optimize the design of a steel structure:
• Performance/cost optimization for a structural steel truss
• Performance optimization for a structural steel high-rise braced frame core
• Comprehensive optimization of a steel grid shell structure
The possibilities of this design approach are only limited by the user’s ambition.
While it is true that the upfront cost associated with learning the approach can be a barrier to entry, the long-term benefit certainly outweighs any initial setback. All projects, regardless of scale, can benefit from this design process and the associated data that becomes available through its use.

Parametric Design, Explained
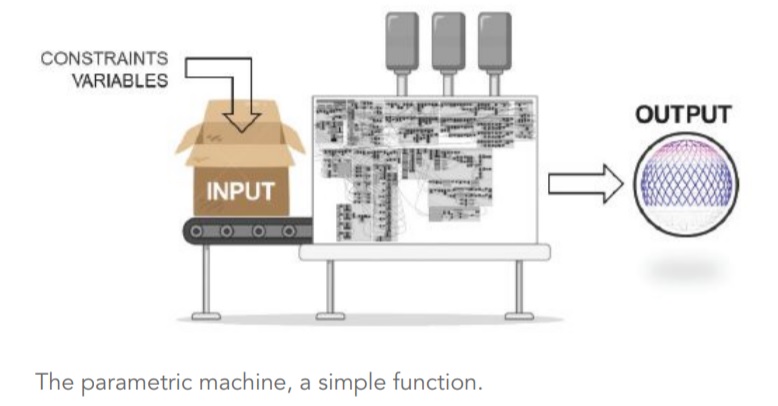
The parametric approach can most easily be understood by looking at the design approach as a mathematical function. The algorithm is the function itself, comprised of constants, variables, and constraints. The parametric aspect of the function is the set of variables being explored and the constraints that these variables must satisfy. Rather than test for validity after output has been obtained, variables are often associated with a domain to ensure that constraints are satisfied. For example, when looking at the design of a simple truss, the span, supports, and loads would be considered constants. The depth of the truss, however, would be considered a variable, hypothetically constrained by the architecture to a depth between 5 ft and 10 ft.
Once the algorithm is assembled, verified, and run to completion, the user has access to the output they set out to obtain. In structural engineering, this output could be a geometric model,
analysis model, member forces, member sizes, etc.
So how can parametric design be used to optimize structures? The process described thus far is manual. The designer develops an algorithm and determines the output they would like to obtain. Should this process continue, they would then be responsible for changing inputs to obtain results for different permutations of the defined variables. This could be a lengthy process depending on the complexity of the algorithm—regardless, this is certainly not the most efficient way to proceed. It is thus in the best interest of the designer to use an evolutionary solver to quickly iterate through the possible solutions.

Evolutionary solvers are not a new concept. The most common example is the Solver add-in for Microsoft Excel. This add-in allows the user to achieve a goal by setting the solver to change the value of certain cells within specified constraints. Similarly, Revit/ Dynamo has an evolutionary solver called “Optimo,” and Rhino/Grasshopper has one called “Galapagos.” While not the only evolutionary solvers available for each of the programs, they are the most common.
An evolutionary solver repeatedly runs a design algorithm until it obtains the closest possible result to the user’s set target. During each of these runs, the solver identifies the specific variable permutations that produce the most favorable results. The favorable permutations are stored and then incorporated within the next generation of the iterative process to improve upon the solution. The outcome is the permutation of variables that results in an output closest to the designer’s set target.
As the goals of individual users can vary widely, a fitness function is commonly applied when using an evolutionary solver. A fitness function takes the user’s goal and converts it to a value to be either maximized or minimized by the solver. The value can be a singular output, such as tonnage or self-weight, or it can be the result of a multi-variable function, such as cost. Though it requires more input from outside parties, cost is often the most impactful fitness function to use when comparing design alternatives within structural engineering. For example, the tonnage of a steel structure is only one component of the total cost. An engineer must also consider fabrication, labor, erection, procurement, etc. Let’s assume a steel structure has the following general costs—acknowledging that both (a) this pricing is theoretical (and may vary based on region) and (b) there will, of course, be others, depending on the project:
Raw material = $2,000/ton = X
Cost per fabricated and erected member = $2,000/piece = Y
Cost per connection = $1,000/connection = Z
The fitness function (FF) for cost therefore becomes:
FF = 2,000 × X + 2,000 × Y + 1,000 * Z
Where X, Y, and Z are outputs of the algorithm.

Parametric Optimization of a Structural Steel Truss
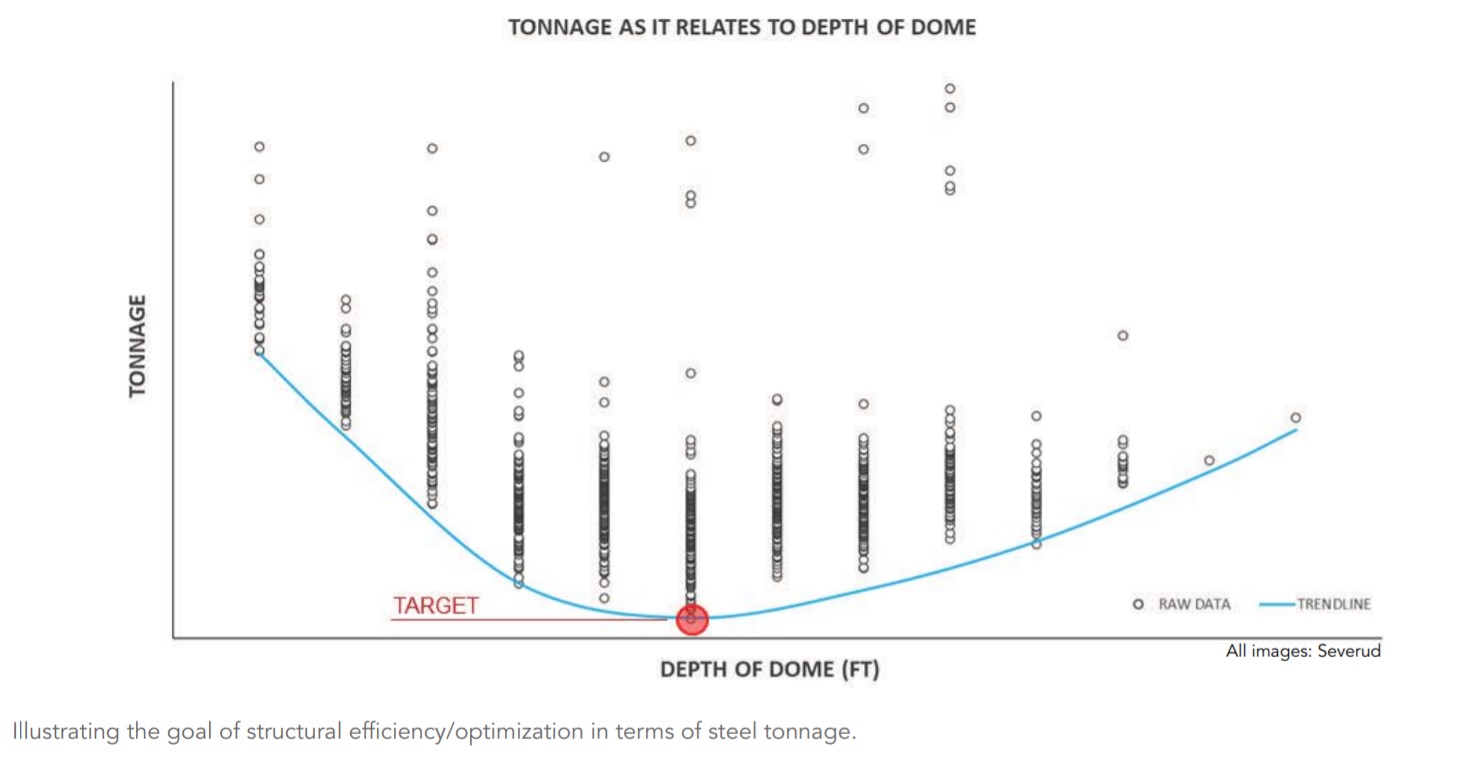
Now let’s run through the first of the three examples we mentioned at the beginning of the article: optimizing a steel truss, adhering to the given constraints, variables,and targets. Constraints:
• Span: 125 ft
• Depth: Minimum of 5 ft, maximum of 25 ft (note that trusses depths are typically 1⁄10 of the span; these numbers simply refer to this example)
• Support condition: Pin-roller
• Load: Dead and live loads are evenly distributed along the top and bottom chords
• Maximum deflection: L/240 (TL)
• Structural steel shapes used:W8, W10, W12, and W14 families Variables:
• Evenly spaced panels (quantity)
• Truss depth variation (in feet) Targets:
• Performance optimization in the form of minimized tonnage
• Cost optimization
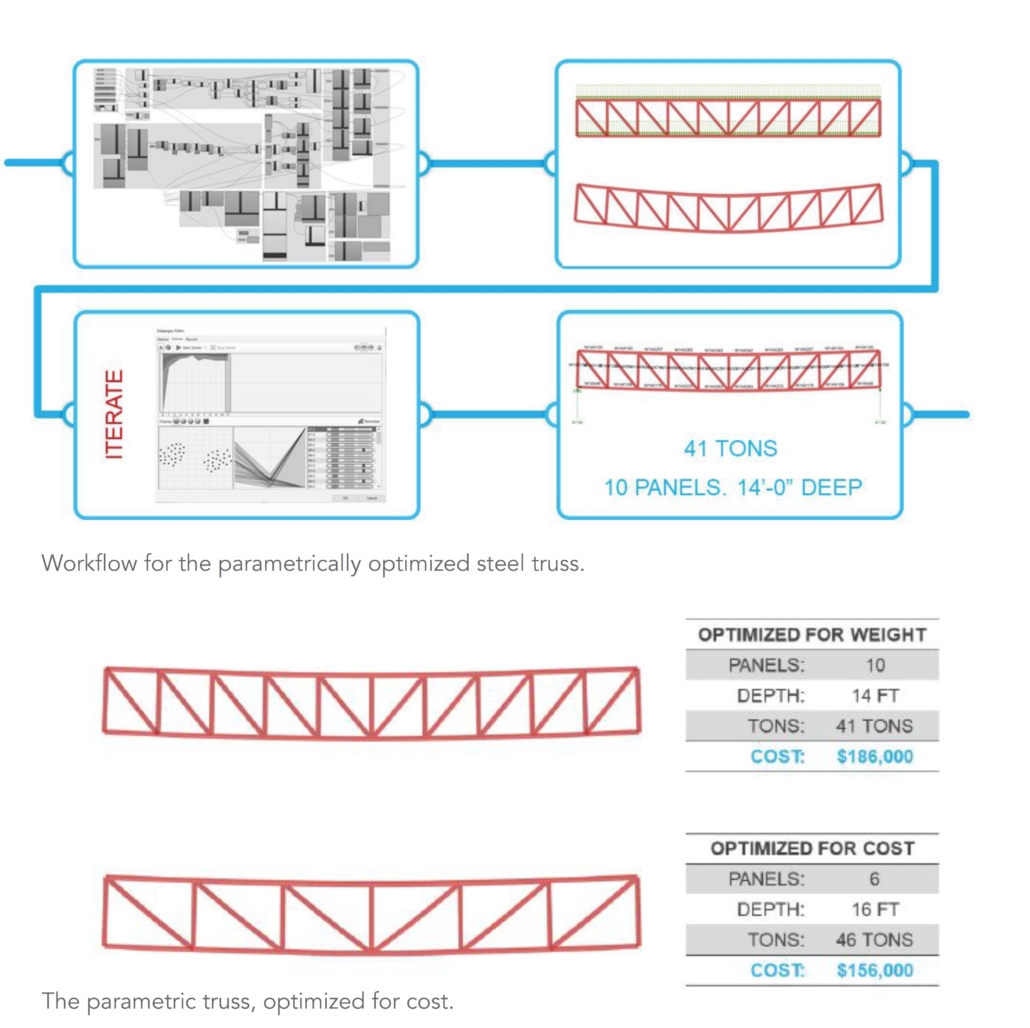
The workflow is similar to the general workflow previously discussed. The algorithm and model are developed in Rhino and Grasshopper. Structural analysis is then performed using Karamba3D. Next,
Galapagos (evolutionary solver) is introduced to the algorithm, and the optimization process is started. Finally, the evolutionary solver converges on the targets, and the optimized result is chosen.
In this case, the optimized result is a10-panel truss that is 14 ft deep and weighs 41 tons. This result, however, does not necessarily coincide with the cost optimization target. The following cost function will be used as the fitness function:
Cost = $2,000/ton raw material + $2,000/ fabricated piece + $1,000/connection
The evolutionary solver is now run to target the truss with the least cost. As expected, the result does not match the truss from the optimization run for least tonnage. The truss optimized for cost has six panels, is 16 ft deep, weighs 46 tons, and costs $156,000. The truss optimized for tonnage costs $186,000.00, so the savings here is $30,000 per truss. In order to be certain that the cost function being used is accurate, it is imperative for the steel fabricator and erector to be involved with the optimization process as early as possible. The client will greatly appreciate the cost savings—and
parametric-enabled projects aside, early collaboration with fabricators and erectors brings benefits to any steel project.

Parametric Optimization of a Structural Steel High-Rise Braced Frame Core
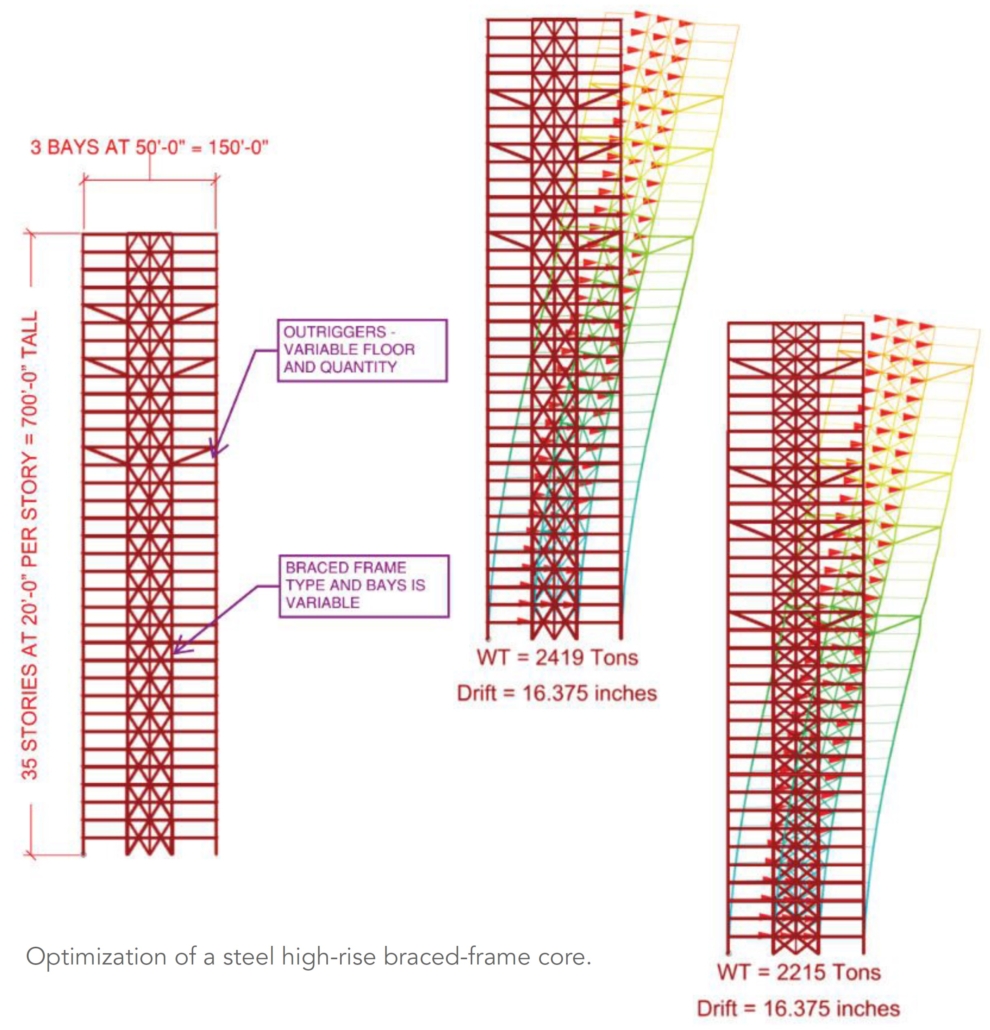
The newest generation of high-rise structures features an aggressive combination of complex geometry and height. This is made possible by recent advancements in materials, construction methods, and analytical procedures. Parametric optimization, when combined with these other advancements, can help engineers identify crucial information regarding design alternatives early in a project. The most effective solutions can thus be implemented without causing delays or other unforeseen complications, and include structural form, bracing and outrigger configurations, custom structural shapes, and more.
In this simplified example, the high-rise structure is a 700-ft-tall, 35-story office building incorporating three structural outriggers. The building is a 150-ft by 150-ft square in plan, and each major-axis direction has three 50-ft bays, the center bay being a 50-ft by 50-ft braced elevator core. The parametric workflow is the same as in the steel truss example, but for simplicity, the optimization only considered structural tonnage.
The results of this example show that by introducing a fourth outrigger, repositioning the outriggers, and changing the bracing configuration, 200 tons of steel can be removed from the building without sacrificing lateral performance.

منبع: مجله Modern Steel Construction

در صورتیکه نیاز به ترجمه این مقاله دارید کلیک کنید